机器学习-决策树分类

文章发布时间:

2025-06-24

最后更新时间:

2025-07-01

文章总字数:

1.6k

预计阅读时间:

6 分钟

决策树-分类

一.概念

决策节点
通过条件判断而进行分支选择的节点
叶子节点
没有子节点的节点，表示最终的决策结果。
决策树的深度
所有节点的最大层次数。根节点的层次数定为0，从下面开始每一层子节点层次数增加,不包括叶子节点
决策树优点：

可视化-可解释能力高-对算力要求低

决策树缺点：

容易过拟合，不要把深度调整太大。

给一个简单的决策树例子：

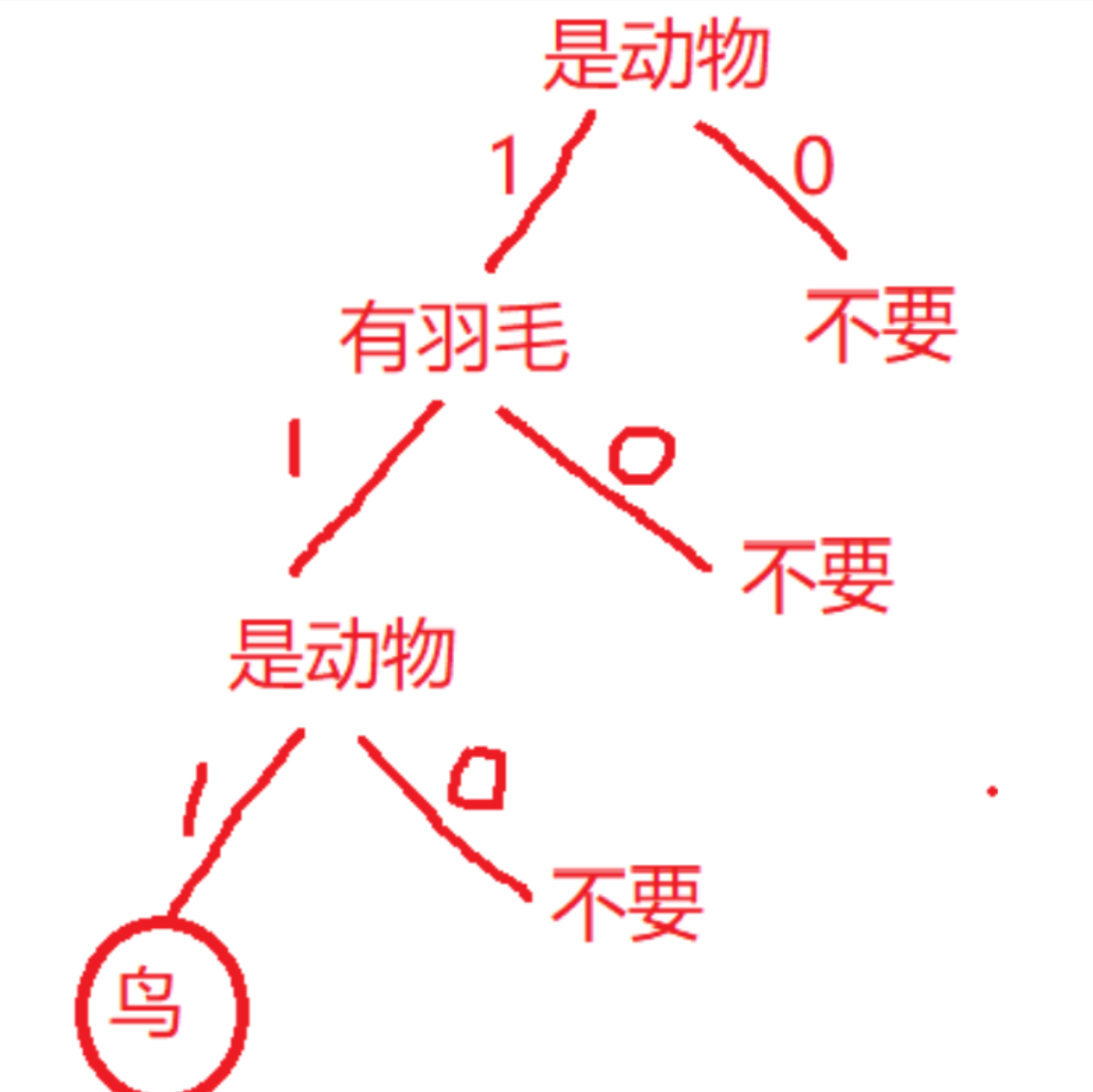
二.基于信息增益决策树的建立

2.1 信息熵

信息熵描述的是不确定性。信息熵越大，不同的数据量越大，不确定性越大。

假设样本某特征或标签共有N类，第k类样本所占比例为:

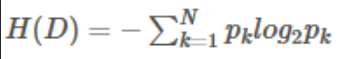
2.2 信息增益(ID3算法会使用)

信息增益是一个统计量，用来描述一个属性区分数据样本的能力。信息增益越大，那么决策树就会越简洁，因为增益越大的决策节点会放在更前面。

信息增益需要信息熵来计算，即用某种特征区分样本标签的信息增益为：

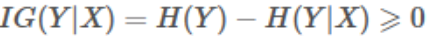
也就是说，先得算标签的信息熵，然后再计算用某个特征区分标签的信息熵，最后再作差。

我们用一个例子来介绍信息增益决策树的建立：

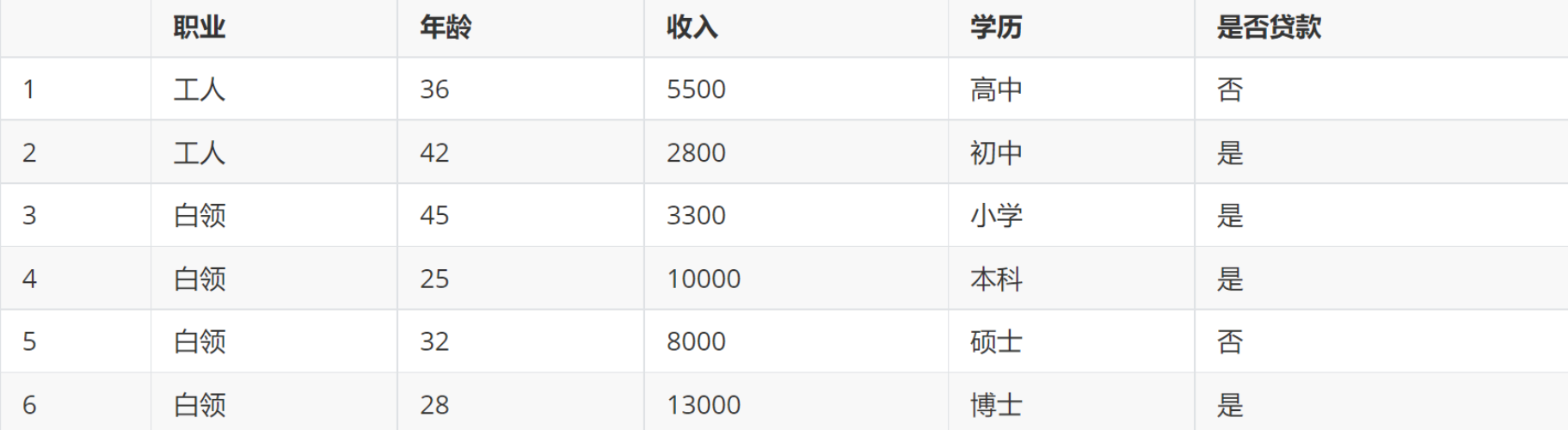
对比属性信息增益发现，”收入”和”学历”相等，并且是最高的，所以我们就可以选择”学历”或”收入”作为第一个决策树的节点（这里是把学历分为两类，如果就直接分类的话，那么每种学历都得单独计算信息增益且可能会单独作为一个决策节点）

注意：此时筛选掉第一个决策节点选择的数据，接下来我们继续重复1，2的做法继续寻找合适的属性节点

三.基于基尼指数决策树的建立(CART算法会使用)

基尼指数（Gini Index）是决策树算法中用于评估数据集纯度的一种度量，基尼指数衡量的是数据集的不纯度，或者说分类的不确定性。

对于多分类问题，如果一个节点包含的样本属于第 k 类的概率是 pk，则节点的基尼指数定义为：

基尼指数越低，代表所有样本类别都基本一致，纯度高。

而基于基尼指数的决策树更简单，假设一个特征有m种不同值，那么就是用这m种值的基尼指数乘以自身占比并求和得到该特征的基尼指数。通过选择最小的基尼指数，得到决策树。

四.两种决策树的API

4.1 模型API

sklearn.tree.DecisionTreeClassifier()

参数：

criterion:
- 当criterion取值为”gini”(默认)时采用基尼不纯度（Gini impurity）算法构造决策树，
- 当criterion取值为”entropy”时采用信息增益（ information gain）算法构造决策树.
max_depth：默认为=None，树的最大深度

# 以信息增益构建决策树
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 构建信息增益决策树
clf = DecisionTreeClassifier(criterion='entropy', max_depth=5)
clf.fit(X_train, y_train)

# 预测测试集
y_pred = clf.predict(X_test)

# 计算准确率
score = clf.score(X_test, y_test)
print('准确率:', score)

结果：

1	`准确率: 0.9777777777777777`

4.2 可视化API

sklearn.tree.export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)

参数：

- estimator决策树预估器

- out_file生成的文档

- feature_names节点特征属性名
-

功能:

把生成的文档打开，复制出内容粘贴到<http://webgraphviz.com>中，点击"generate Graph"会生成一个树型的决策树图。

# 以信息增益构建决策树
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import export_graphviz

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 构建信息增益决策树
clf = DecisionTreeClassifier(criterion='entropy', max_depth=5)
clf.fit(X_train, y_train)

# 可视化
export_graphviz(clf, out_file='tree.dot', feature_names=['花瓣长度', '花萼宽度', '花瓣长度', '花瓣宽度'])

五.集成学习方法之随机森林

5.1 基本概念

集成学习是机器学习一个大方向，基本思想就是将多个分类器组合，从而实现一个预测效果更好的集成分类器。

其特点为：

每次有放回地从训练集中取出 n 个训练样本，组成新的训练集；
利用新的训练集，训练得到M个子模型；
对于分类问题，采用投票的方法，得票最多子模型的分类类别为最终的类别。

随机森林就属于集成学习,是通过构建一个包含多个决策树(通常称为基学习器或弱学习器)的森林，每棵树都在不同的数据子集和特征子集上进行训练，最终通过投票或平均预测结果来产生更准确和稳健的预测。

下图是其算法原理：

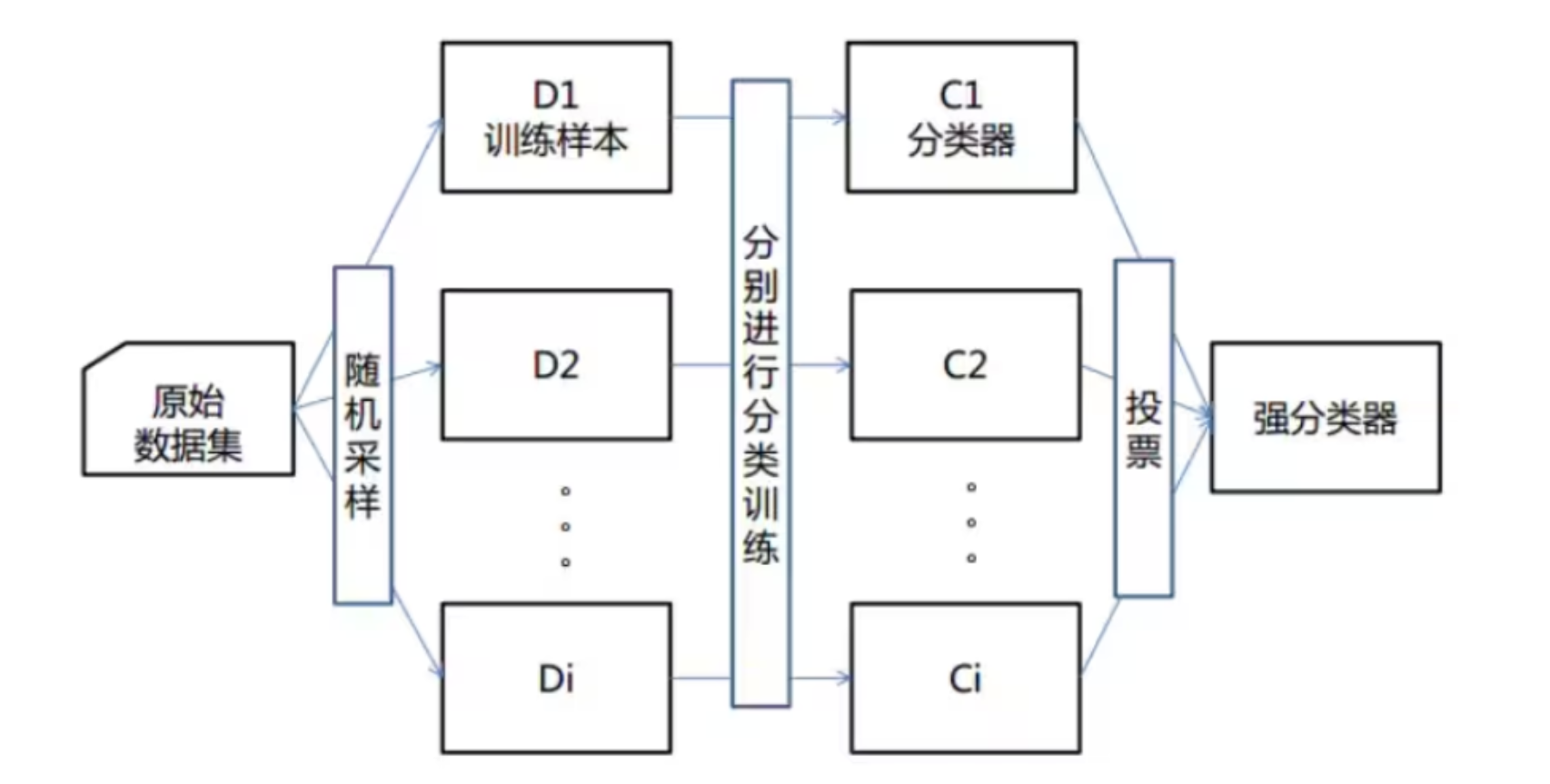
但其为什么叫随机森林呢？随机性就在特征随机，训练集随机上。

训练集随机就是上面讲过的有放回地取出n个训练样本组成一个新训练集；

特征随机就是在每棵树的训练过程中，对特征进行随机选择，可以是一个，也可以是多个。

5.2 API

sklearn.ensemble.RandomForestClassifier

参数：

n_estimators:决策树个数,默认100
criterion：{“gini”, “entropy”}
max_depth：树的最大深度。

# 随机森林预测
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 随机森林预测
rf = RandomForestClassifier(n_estimators=100, random_state=42)
rf.fit(X_train, y_train)

# 预测
data_new = [[5.1, 3.5, 1.4, 0.2]]
new_pred = rf.predict(data_new)
print("预测结果:", new_pred)
# 评估模型
score = rf.score(X_test, y_test)
print("准确率:", score)

结果：

1 2	`预测结果: [0] 准确率: 1.0`

≡