一.拟合

1.1 欠拟合

指模型在训练数据上表现不佳，同时在新的未见过的数据上也表现不佳。一般是：

• 训练误差较高。

• 测试误差同样较高。

原因：模型可能过于简化，数据太少，不能充分学习训练数据中的模式。

1.2 过拟合

在训练数据上表现得非常好，但在新的未见过的数据上表现较差。一般是：

• 训练误差非常低。

• 测试误差较高。

原因：模型过于复杂，w过多，学习到了训练数据中的噪声规律。

1.3 正则化

正则化就是防止过拟合，增加模型的鲁棒性。若两个模型损失都一样，就要看哪个模型的鲁棒性更好。也就是看两个模型对有部分错误的数据集的预测效果如何，如果效果依然不错，那么鲁棒性就好。一般模型参数w越小，同等损失下，鲁棒性越好。那我们既需要模型误差小，又得让鲁棒性更好怎么办？

这就是正则化的工作。

正则化本质就是牺牲模型在训练集上的正确率来提高推广、泛化能力。将原来的损失函数加上一个惩罚项（正则化函数）组成新损失函数，让新损失更小，即让计算出来的模型W相对更小一些，就是正则化

常用的惩罚项有L1正则项或者L2正则项:

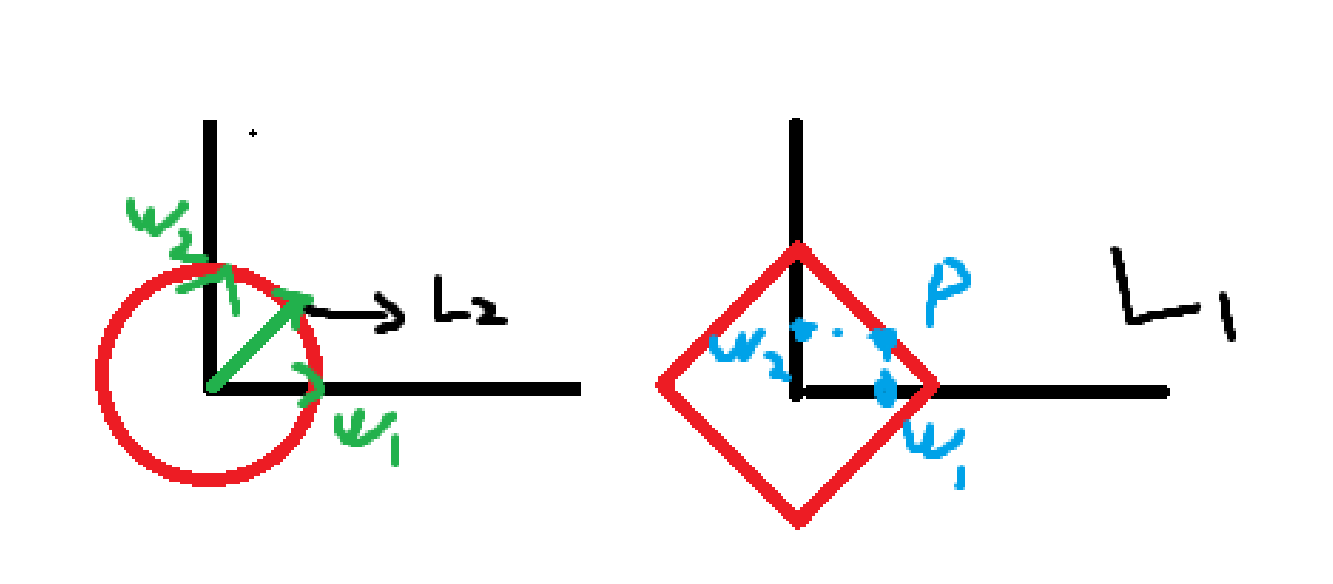
$L1=||w||1=\textstyle\sum{i=1}^{n}|w_i|$ 对应曼哈顿距离

$L2=||w||2=\textstyle\sqrt[p]{\sum{i=1}^{n}x^p_i,X=(x_1,x_2,…x_n)}$ 对应欧氏距离

其实L1和L2正则的公式在数学里面的意义就是范数,代表空间中向量到原点的距离

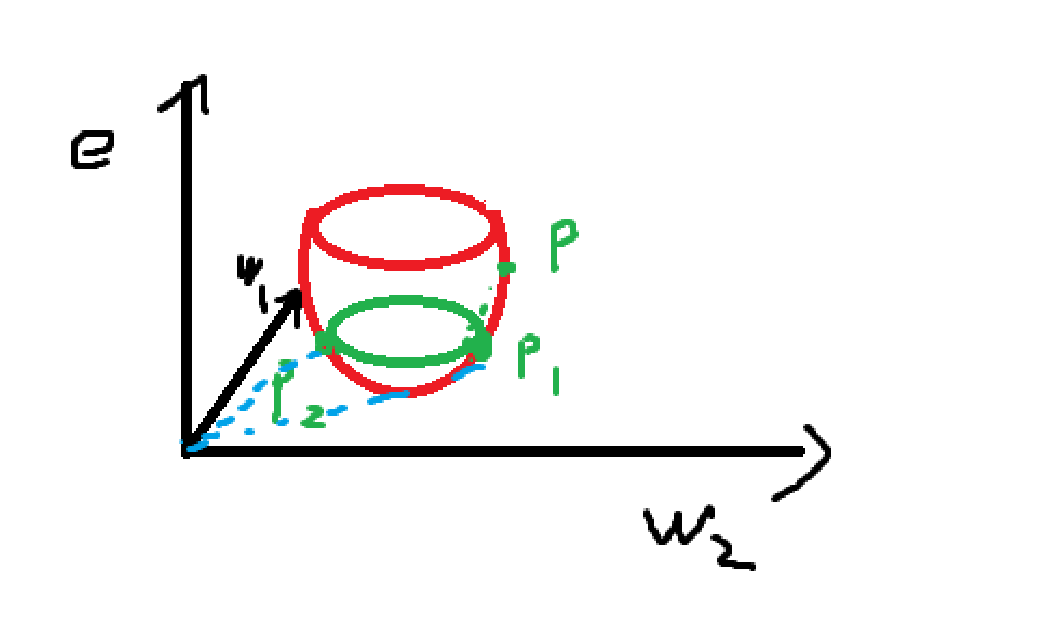
上图以L2正则化为例，蓝色虚线直观体现正则化的作用。由p点进行梯度下降到P1，没有正则化就会到此为止。加入L2正则化后，其会选择更靠近原点的P2，使得w向量更小。

当我们把多元线性回归损失函数加上L2正则的时候，就诞生了Ridge岭回归。当我们把多元线性回归损失函数加上L1正则的时候，就孕育出来了Lasso回归。还记得我们之前讲过的损失等高线吗？由于原损失函数加上惩罚项之后图像我们是难想象的，所以我们把损失函数和惩罚项分别画出来，方便理解：

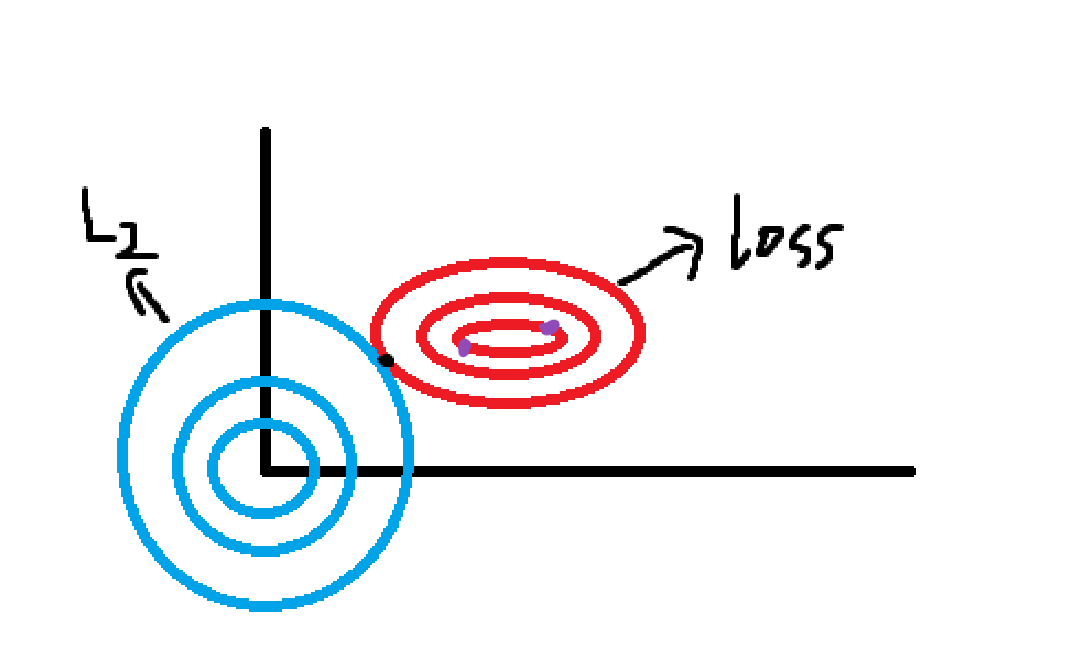
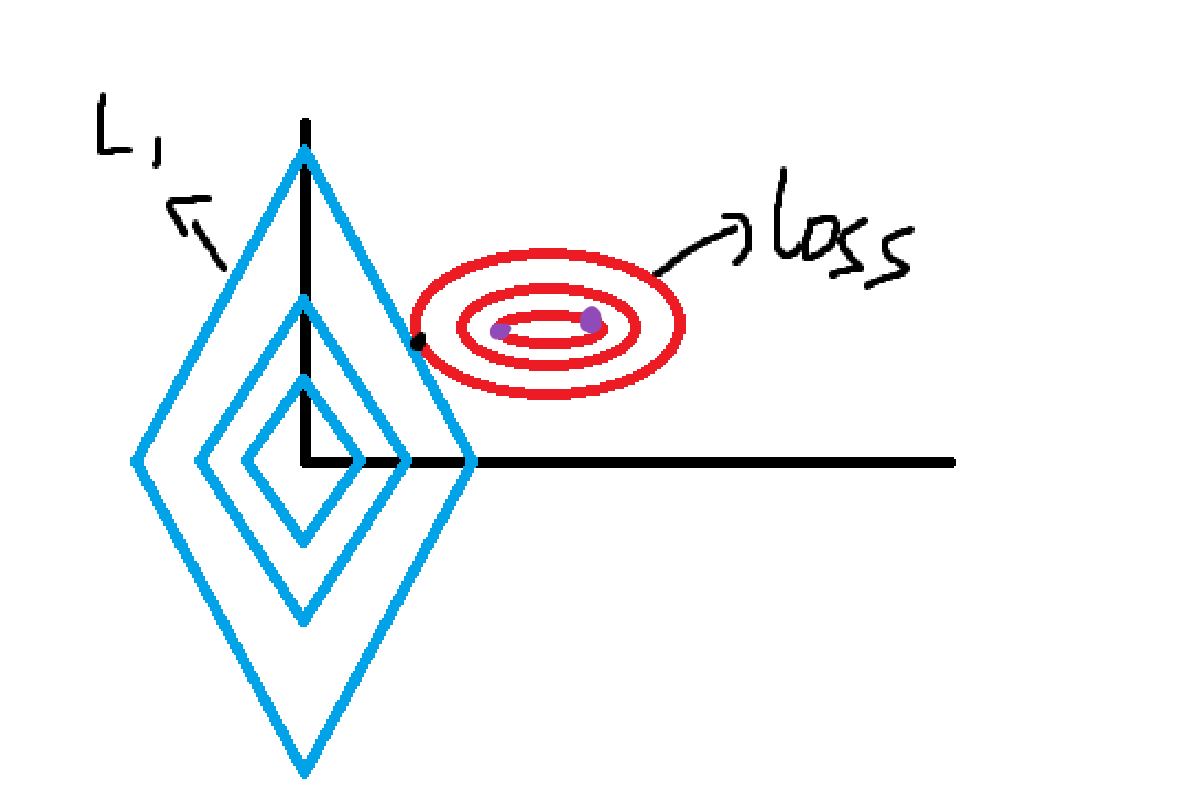
图中横纵坐标轴是w1，w2，蓝色就是L2与L1正则化的函数图像，等高线是损失函数loss，紫色是loss相同的两点。我们的目的是让loss加正则化函数的整体变小，那两个函数都得尽量小，成反比的两个函数值就得达到一个平衡点，也就是两个函数图像相交的点，到两个图像的中心即原点和等高线最低点都要尽可能的近。那么显而易见，我们就会选择更靠向原点的紫色点。