机器学习-sklearn梯度下降

文章发布时间:

最后更新时间:

文章总字数:
2.2k

预计阅读时间:
9 分钟

sklearn 梯度下降

官方的梯度下降API常用有三种:

  • 批量梯度下降BGD(Batch Gradient Descent)

  • 小批量梯度下降MBGD(Mini-BatchGradient Descent)

  • 随机梯度下降SGD(Stochastic Gradient Descent)。

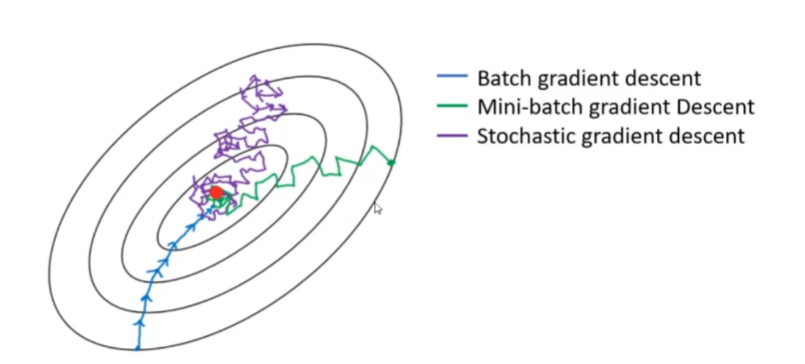
上面的图中，描述的正是三种梯度下降算法实现的过程，黑色等高线代表损失。接下来我们详细讲讲：

一.批量梯度下降BGD

其使用整个训练数据集来计算梯度并更新模型参数，这也就是我们之前用的算法。每一次迭代都使用所有数据来进行训练（构建损失函数），这使得更新方向更加准确，但计算成本较高，且一个很大的缺点是需要在内存中存储整个数据集，对于大型数据集来说可能成为一个问题。

而且BGD是没有专门的API函数的，所以只能自己实现，包括损失函数的计算，梯度的计算以及权重更新的代码都要自己写。

二.随机梯度下降SGD

每一步更新参数时，仅使用单个训练样本，用这个样本计算梯度，然后更新参数w，直到一轮训练epoch完成,即整个数据集被遍历完一次。

每一次更新用的都是上一个样本更新的w,来计算这一次选择的样本的梯度，然后再更新w。

后期能够很好地解决局部最优解的问题。然而，由于每次只使用一个样本进行更新，梯度估计可能较为嘈杂，这可能导致更新过程中出现较大的波动。在实际应用中，可以通过减少学习率（例如采用学习率衰减策略）来解决。

注意：

  • 学习率 alpha: 需要适当设置，太大会导致算法不收敛，太小则收敛速度慢。

  • 随机性: 每次迭代都从训练集中随机选择一个样本，这有助于避免陷入局部最小值。

  • 停止条件: 可以是达到预定的最大迭代次数，或者梯度的范数小于某个阈值。

API:

sklearn.linear_model.SGDRegressor()

参数:

  • loss: 损失函数，默认为 squared_error

  • fit_intercept: 是否计算偏置，default=True

  • eta0:学习率初始值，默认0.01

  • learning_rate:

    • constant: eta = eta0 学习率为eta0设置的值，保持不变

    下面的三种都是让学习率不断减小，只是公式不同：

    • optimal: eta = 1.0 / (alpha * (t + t0))
    • invscaling（默认）: eta = eta0 / pow(t, power_t)
    • adaptive: eta = eta0, 学习率由eta0开始，逐步变小

  • max_iter: 取数据的次数，default=1000

  • shuffle=True 每批次是否洗牌

  • penalty（暂时不用管）:要使用的惩罚(又称正则化项)

    默认为’ l2 ‘，这是线性SVM模型的标准正则化器。

    ‘ l1 ‘和’ elasticnet ‘可能会给模型(特征选择)带来’ l2 ‘无法实现的稀疏性。

    当设置为None时，不添加惩罚。

属性：

  • coef_ 回归后的权重系数

  • intercept_ 偏置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 线性回归 加载糖尿病数据集，进行回归预测
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error

from sklearn.datasets import load_diabetes
# 加载数据
diabetes = load_diabetes()
print(diabetes)
# 划分训练集与测试集
x_train, x_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, random_state=22)
# 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 线性回归预估器
estimator = SGDRegressor(learning_rate="constant", eta0=0.01, max_iter=10000,loss="squared_error")

estimator.fit(x_train, y_train)

# 得出模型
print("权重系数为：\n", estimator.coef_)  #权重系数与特征数一定是同样的个数。
print("偏置为：\n", estimator.intercept_)

# 模型评估
y_predict = estimator.predict(x_test)
print("预测的数据集：\n", y_predict)
print("得分:\n",estimator.score(x_test, y_test))
error = mean_squared_error(y_test, y_predict)
print("均方误差为：\n", error)

结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
{'data': array([[ 0.03807591,  0.05068012,  0.06169621, ..., -0.00259226,
         0.01990749, -0.01764613],
       [-0.00188202, -0.04464164, -0.05147406, ..., -0.03949338,
        -0.06833155, -0.09220405],
       [ 0.08529891,  0.05068012,  0.04445121, ..., -0.00259226,
         0.00286131, -0.02593034],
       ...,
       [ 0.04170844,  0.05068012, -0.01590626, ..., -0.01107952,
        -0.04688253,  0.01549073],
       [-0.04547248, -0.04464164,  0.03906215, ...,  0.02655962,
         0.04452873, -0.02593034],
       [-0.04547248, -0.04464164, -0.0730303 , ..., -0.03949338,
        -0.00422151,  0.00306441]], shape=(442, 10)), 'target': array([151.,  75., 141., 206., 135.,  97., 138.,  63., 110., 310., 101.,
        69., 179., 185., 118., 171., 166., 144.,  97., 168.,  68.,  49.,
        68., 245., 184., 202., 137.,  85., 131., 283., 129.,  59., 341.,
        87.,  65., 102., 265., 276., 252.,  90., 100.,  55.,  61.,  92.,
       259.,  53., 190., 142.,  75., 142., 155., 225.,  59., 104., 182.,
       128.,  52.,  37., 170., 170.,  61., 144.,  52., 128.,  71., 163.,
       150.,  97., 160., 178.,  48., 270., 202., 111.,  85.,  42., 170.,
       200., 252., 113., 143.,  51.,  52., 210.,  65., 141.,  55., 134.,
        42., 111.,  98., 164.,  48.,  96.,  90., 162., 150., 279.,  92.,
        83., 128., 102., 302., 198.,  95.,  53., 134., 144., 232.,  81.,
       104.,  59., 246., 297., 258., 229., 275., 281., 179., 200., 200.,
       173., 180.,  84., 121., 161.,  99., 109., 115., 268., 274., 158.,
       107.,  83., 103., 272.,  85., 280., 336., 281., 118., 317., 235.,
...
得分:
 0.4759617296042802
均方误差为：
 3208.299159729948

三.小批量梯度下降MBGD

小批量梯度下降是一种介于批量梯度下降（BGD）与随机梯度下降（SGD）之间的优化算法，它结合了两者的优点，在机器学习和深度学习中被广泛使用。

基本思想是在每个迭代步骤中使用一小部分（即“小批量”）训练样本来计算损失函数的梯度，并据此更新模型参数。小批量梯度下降能够在保持较快的收敛速度的同时，维持相对较高的稳定性。且MBGD和SGD都有几个优点：

  1. 减少内存需求

  2. 可以进行分布式训练：因为一般数据集很大，数据都是存在磁盘中，每次使用取一部分出来。只取一条或者一批数据方便几台电脑同时训练一个大数据集

  3. 在线学习：可以随时训练，即使用原数据开始训练时，另一个新的数据集也可以加入训练中

但由于没有BGD的API，所以只能用SGD来实现。但严格来说这样实现的也不是MBGD的算法思想，而是另一种接近的思想。

注意：我们分批次（batch）地训练模型，调用partial_fit函数训练会直接更新权重,而不需要调fit从头开始训练。

fit()是不用自己设置迭代次数的，max_iter就能控制迭代次数。而partial_fit()每次只能训练一批数据，迭代需要自己实现，max_iter不起作用。所以每一批次的训练需要自己来用for循环实现，所有批次遍历完就是一个epoch。只使用SGD的话，也就是使用fit会使用其中默认的batch_size=1，即每次迭代训练一个样本。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
# 具体实现方法
# 线性回归 加载糖尿病数据集，进行回归预测
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import  SGDRegressor
from sklearn.metrics import mean_squared_error
import numpy as np
import math
import time
import os
import joblib

from sklearn.datasets import load_diabetes
diabetes = load_diabetes()

# 若本地有模型，选择获取
model_path=os.path.join(os.path.dirname(__file__),'../model',"mbgd_regressor_model.pkl")
transfer_path=os.path.join(os.path.dirname(__file__),'../model',"mbgd_transfer.pkl")

model=None
transfer=None
# 根据模型再本地是否存在，选择两种模型加载方式
if os.path.exists(model_path):
    model=joblib.load(model_path)
    transfer=joblib.load(transfer_path)
else:
    model=SGDRegressor(fit_intercept=False,loss="squared_error",max_iter=100,eta0=0.001,learning_rate="constant")
    transfer=StandardScaler()

# 划分训练集与测试集
x_train, x_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, random_state=22)

# 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 定义超参数
batch_size = 32  # 批量大小
epochs = 100  # 迭代次数

# 线性回归预估器
model = SGDRegressor(fit_intercept=False,learning_rate="constant", eta0=0.001, max_iter=100,shuffle=True)

# 批次数量,向上取整
n_batches = math.ceil(len(x_train) / batch_size)  

# 这个循环是迭代次数的体现
for epoch in range(epochs):
    # 随机打乱样本顺序
    indices = np.arange(len(x_train))
    np.random.shuffle(indices)
    start_time = time.time()
    

    # 这个循环是为了把每个批次都取一遍，因为把所有数据都取一次才算一次迭代epoch
    for i in range(n_batches):
        start_idx = i * batch_size
        # 因为最后一批可能不足一个batch_size，所以要用min函数
        end_idx = min((i + 1) * batch_size,len(x_train))
        batch_indices = indices[start_idx:end_idx]
        X_batch = x_train[batch_indices]
        y_batch = y_train[batch_indices]
        model.partial_fit(X_batch, y_batch)  # 更新模型权重

    score = model.score(x_test, y_test)
    # 打印每一轮的评分与训练时间
    print(f"训练轮次:{epoch} / {epochs}, score:{score}, 训练时间:{time.time() - start_time}s")

    # 保存模型
    joblib.dump(model,model_path)
    joblib.dump(transfer,transfer_path)
  
# 得出模型
print("权重系数为：\n", model.coef_)  #权重系数与特征数一定是同样的个数。

# 模型评估
y_predict = model.predict(x_test)
error = mean_squared_error(y_test, y_predict)
print("均方误差为：\n", error)

# 预测
def detect():
    model=joblib.load(model_path)
    transfer=joblib.load(transfer_path)
    x_true=[[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0]]
    x_true=transfer.transform(x_true)
    print(model.predict(x_true))

if __name__ == '__main__':
    detect()

以后梯度下降都是用的MBGD方法，且上面的代码就是机器学习及深度学习的基本步骤。

四.梯度下降优化

4.1 标准化

针对数据方面的问题优化

4.2 正则化

针对模型方面的问题优化，把模型变简单

≡