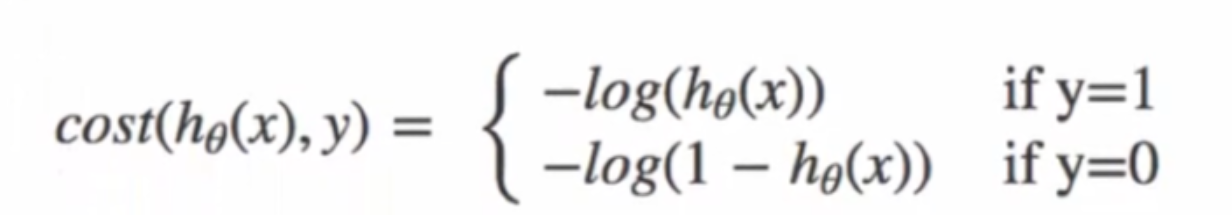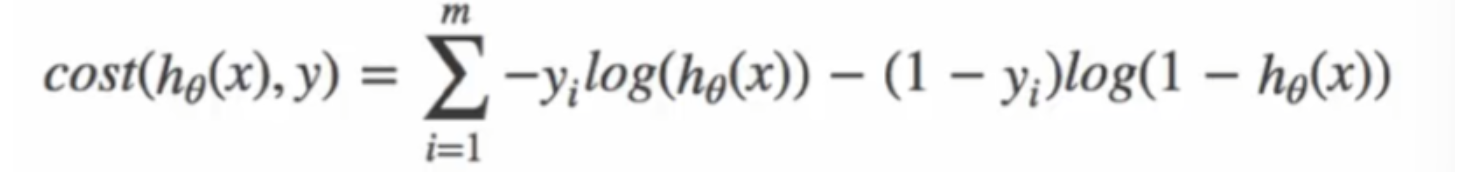机器学习-逻辑回归

文章发布时间:

最后更新时间:

文章总字数:
913

预计阅读时间:
3 分钟

逻辑回归

一.概念

逻辑回归是一种分类算法，其内部有回归算法（本质上只是线性回归加了一个sigmod激活函数），但解决的是分类问题。

二.原理

sigmod函数本质把传入的数据变成概率。sigmod也是一种复合即非线性函数，从图像也能看出。

实际上二分类问题中，预测的标签只有两种，而sigmod将线性回归函数的输出转换为一个[0,1]的值，每个转换的值就会与二分类标签0，1有误差，也就可以据此计算误差。

首先要明白，MSE是可以用在分类问题上的，但是是很慢的，一般都不用。所以就有了下面的方法：

考虑到每种标签对应的损失不同，综合下来的二分类损失函数就是（二分类交叉熵损失函数）：

把所有样本的损失值加起来，就是综合的损失。之后只需要慢慢把总损失慢慢减小，就可以让二分类预测的两个类别都预测的更准确。

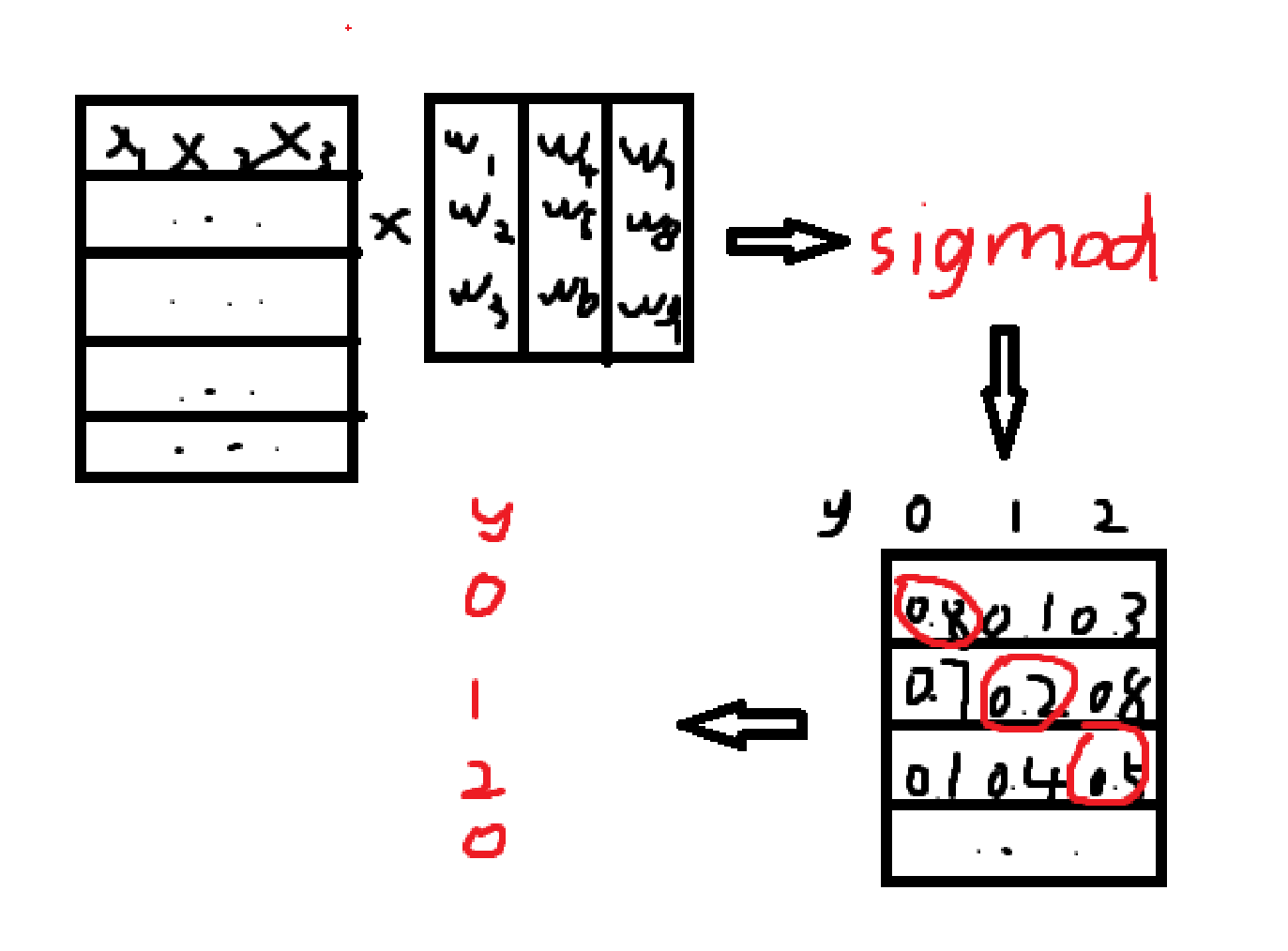
逻辑回归背后的原理：

针对一条新数据，我们会选取概率最大的那个类别作为它的类别。

API：

sklearn.linear_model.LogisticRegression()

参数:

  • fit_intercept： bool, default=True 指定是否计算截距

  • max_iter： int, default=100 最大迭代次数。迭代达到此数目后，即使未收敛也会停止。

模型对象:

  • .coef_ 权重

  • .intercept_ 偏置

  • predict()预测分类

  • predict_proba()预测分类(对应的概率)

  • score()准确率

这里进行w权重计算使用的是编程内的 X 乘（对应位置相乘），而非数学上的矩阵乘法，因此w一般是横着写的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
# 逻辑回归 加载鸢尾花数据集，进行回归预测
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import  SGDRegressor,LogisticRegression
from sklearn.metrics import mean_squared_error
import numpy as np
import math
import time
import os
import joblib

from sklearn.datasets import load_iris
iris= load_iris()

# 若本地有模型，选择获取
model_path=os.path.join(os.path.dirname(__file__),'../model',"luoji_model.pkl")
transfer_path=os.path.join(os.path.dirname(__file__),'../model',"luoji_transfer.pkl")

model=None
transfer=None

# 根据模型再本地是否存在，选择两种模型加载方式
if os.path.exists(model_path):
    model=joblib.load(model_path)
    transfer=joblib.load(transfer_path)
else:
    model=LogisticRegression(fit_intercept=False,max_iter=100)
    transfer=StandardScaler()

# 划分训练集与测试集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 定义超参数
batch_size = 32  # 批量大小
epochs = 100  # 迭代次数


# 批次数量,向上取整
n_batches = math.ceil(len(x_train) / batch_size)  

# 这个循环是迭代次数的体现
for epoch in range(epochs):
    # 随机打乱样本顺序
    indices = np.arange(len(x_train))
    np.random.shuffle(indices)
    start_time = time.time()
    

    # 这个循环是为了把每个批次都取一遍，因为把所有数据都取一次才算一次迭代epoch
    for i in range(n_batches):
        start_idx = i * batch_size
        # 因为最后一批可能不足一个batch_size，所以要用min函数
        end_idx = min((i + 1) * batch_size,len(x_train))
        batch_indices = indices[start_idx:end_idx]
        X_batch = x_train[batch_indices]
        y_batch = y_train[batch_indices]
        model.fit(X_batch, y_batch)  # 更新模型权重

    score = model.score(x_test, y_test)
    # 打印每一轮的评分与训练时间
    print(f"训练轮次:{epoch} / {epochs}, score:{score}, 训练时间:{time.time() - start_time}s")

    # 保存模型
    joblib.dump(model,model_path)
    joblib.dump(transfer,transfer_path)
  
# 得出模型
print("权重系数为：\n", model.coef_)  #权重系数与特征数一定是同样的个数。

# 模型评估
y_predict = model.predict(x_test)
error = mean_squared_error(y_test, y_predict)
print("均方误差为：\n", error)

# 预测
def detect():
    model=joblib.load(model_path)
    transfer=joblib.load(transfer_path)
    x_true=[[0.1,0.2,0.3,0.4]]
    x_true=transfer.transform(x_true)
    print(model.predict(x_true))

if __name__ == '__main__':
    detect()
≡