机器学习-最小二乘法
文章发布时间:
最后更新时间:
文章总字数:
预计阅读时间:
最后更新时间:
文章总字数:
633
预计阅读时间:
2 分钟
最小二乘法
一.基本素养

观察一下上面的内容,这都是最小二乘法所需的条件(不必牢记,因为后期会用更好的方法)。
二.最小二乘法的推导


这个公式很容易推出来,把各个矩阵相乘,最后根据欧几里得范数的平方即可证明。
我们的目的是为了让损失变小,而最小二乘法就求出了损失最小时的w回归系数。可以看到,最小二乘法将原本MSE公式中的1/n改为1/2,那么为什么要这样做呢?又如何让损失loss最小呢?我们基本都会先进行求导:
这里补充一点,一个只有一列的矩阵与其转置左乘就会得到一个只含一个元素的矩阵,这个元素便是欧几里得范数的平方计算的结果。于是把上面的公式拆分:
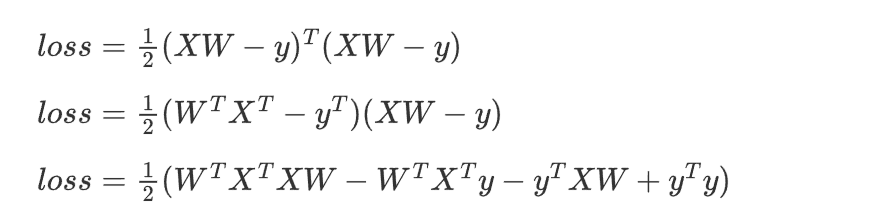
此时进行求导,可是不会求矩阵运算的导数怎么办?没关系,上面已经给出了公式,我们直接代入即可(这里不详细演算,比较麻烦,过程在下面):

接下来我们介绍另一种方法,链式求导(后期深度学习基本都用):
比如这里的loss = 1/2 * ||(Xw - y)|| ** 2
我们假设u = Xw - y,那么loss = 1/2 * ||u|| ** 2
那么loss对w的导数为:(也需要上面的导数公式)
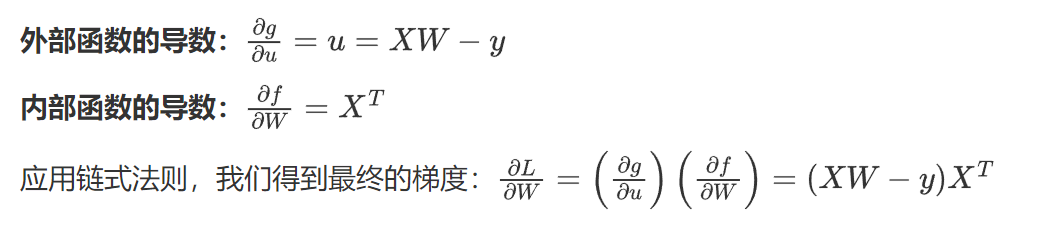
这会儿就明白最小二乘法为什么要是2,因为让损失函数最小跟其前的1/n没有关系,只和w有关,且求导之后其前的系数变成了1,没有多余的复杂度了。
这样我们就求出了w。
三.API
sklearn.linear_model.LinearRegression()
参数:
- fit_intercept:是否计算此模型的截距(偏置)。默认True,如果设置为False,则在计算中将不使用截距(即,数据应中心化)。
属性:
coef_ 回归后的权重系数
intercept_ 偏置(也就是下面w0和x0相乘)
1 | |
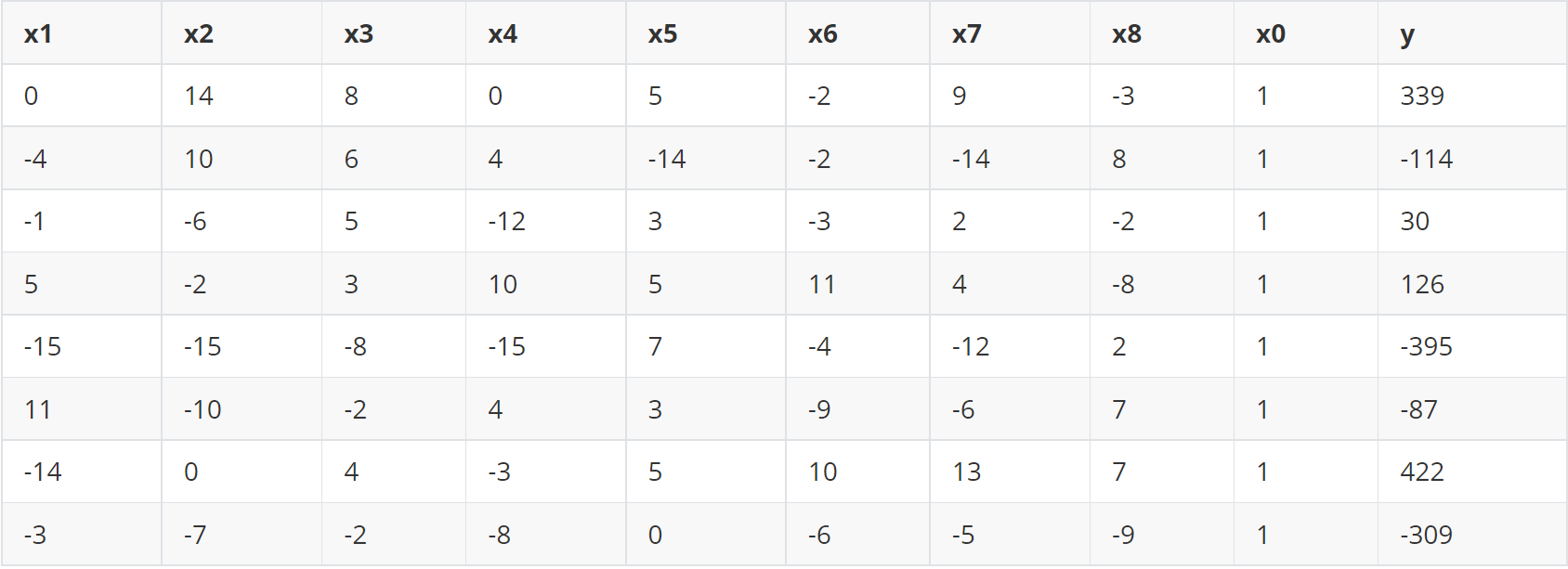
1 | |
结果:
1 | |