梯度下降
一.概念
之前利用最小二乘法求解W有最优解,原因是MSE这个损失函数是凸函数(有唯一极值)。但机器学习损失函数并非都是凸函数,设置导数为0会得到很多个极值。MSE还有一个问题,当数据量和特征较多时,矩阵计算量太大。
给大家介绍一下时间复杂度,就明白之前求解w的算法比较麻烦了:
使用正规方程$W=(X^TX)^{-1}X^Ty$ 求解要求X的特征维度$(x_1,x_2,x_3…)$ 不能太多,逆矩阵运算时间复杂度为$O(n^3)$ , 也就是说如果特征x的数量翻倍,计算时间就是原来的$2^3$倍。很多时候数据量都会破万,此时的计算量太大,已有算力无法支持。
因此我们引入了梯度下降:
比如我心想一个数字,让你来猜,每次猜完我都告诉你大了还是小了,循环往复,你就能猜到我心中的数。这就是梯度下降的例子。如下图:
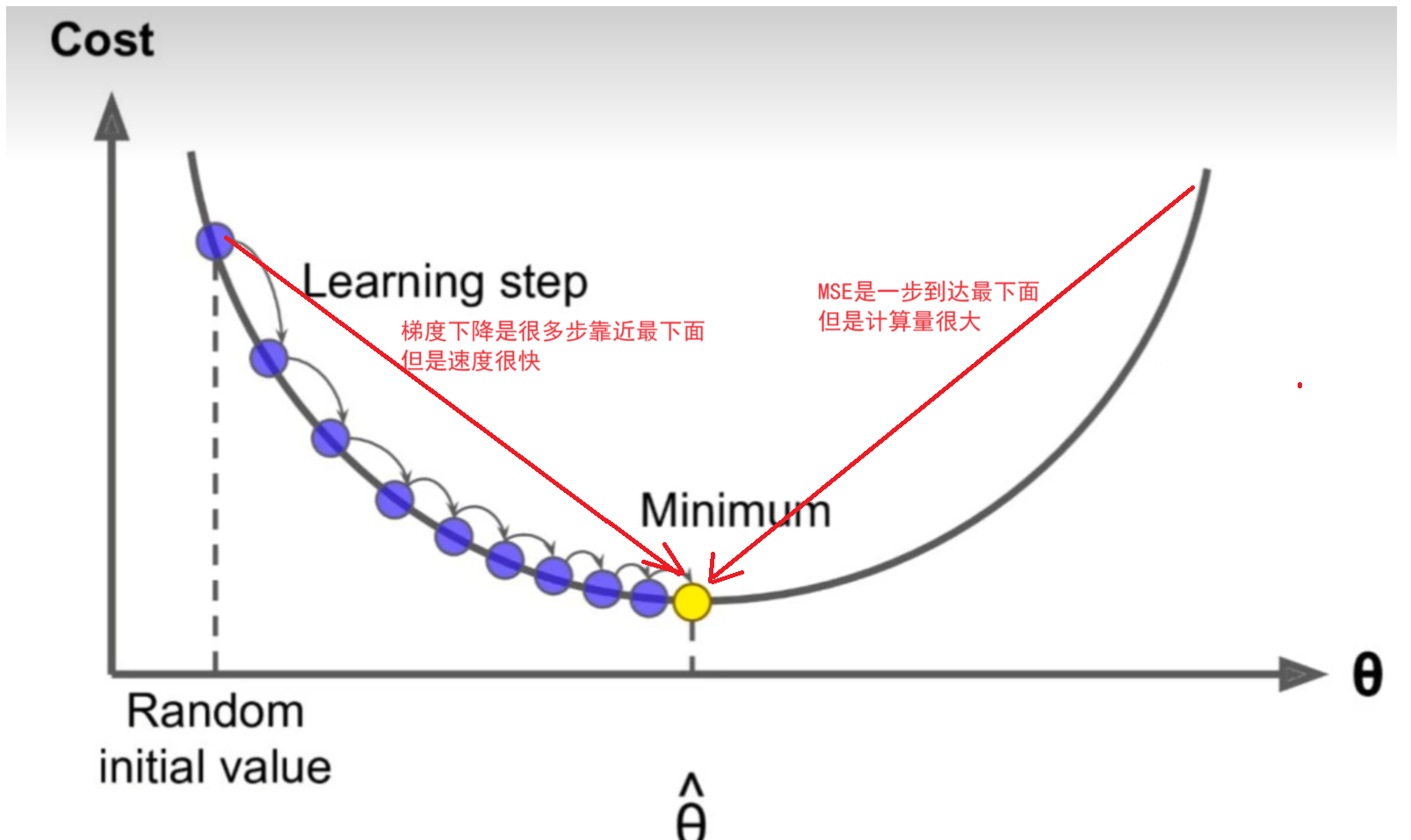
其中random initial value是随机初始化的起始值,也就是在初始化值开始寻找最小的梯度也就是导数。这幅图里只有一个回归系数w,其损失函数MSE就是一个抛物线。而抛物线一点作切线就是该点的梯度即导数,最优w梯度为0,左侧是负数,右侧是正数。而接下来,我们会一步一步往梯度为0的方向寻找w,直到达到收敛。(这里的梯度下降都是针对损失函数)
二.步骤
1、Random随机数生成初始W,随机生成一组成正太分布的数值w0,w1,w2….wn
2、求梯度g,梯度代表曲线某点上的切线的斜率,沿着切线往下就相当于沿着坡度最陡峭的方向下降.
3、if g < 0,w变大,if g > 0,w变小
4、判断是否收敛,如果收敛跳出迭代,如果没有达到收敛,回第2步再次执行2~4步收敛的判断标准是:随着迭代进行查看损失函数Loss的值,变化非常微小甚至不再改变,即认为达到收敛
5.上面第4步也可以固定迭代次数,如果学习率低了,一般都会把迭代次数设置多一点。
三.公式

四.学习率
学习率与梯度下降的幅度直接相关,一般我们会把学习率设置成一个小数,0.1、0.01、0.001、0.0001,也可以设置成随着迭代次数增多学习率逐渐变小
五.自己实现梯度下降
一般来说梯度下降有不同的算法实现,再学习这些算法之前可以先自己手动实现试试:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
import numpy as np
import matplotlib.pyplot as plt
def model(x, w):
return x * w
def loss(w):
return 10 * w**2 - 15.9 * w + 6.5
def gradient(w):
return 20 * w - 15.9
a = np.linspace(-10, 10, 1000)
w = np.random.randint(-10,10)
ws = np.array([])
alpha = 0.01
t = 1000
for i in range(t):
grad = gradient(w)
w = w - alpha * grad
ws = np.append(ws,w)
loss_value = loss(w)
print("第{}次迭代,损失为:{}".format(i+1, loss_value))
print("w的值为:{}".format(w))
plt.plot(a, loss(a), label='损失函数')
plt.plot(ws,loss(ws), label='回归直线')
plt.show()
|
结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| 第1次迭代,损失为:147.32871
w的值为:-3.041
第2次迭代,损失为:94.35508440000001
w的值为:-2.2738
第3次迭代,损失为:60.451964016
w的值为:-1.66004
第4次迭代,损失为:38.75396697024
w的值为:-1.169032
第5次迭代,损失为:24.8672488609536
w的值为:-0.7762256000000001
第6次迭代,损失为:15.979749271010306
w的值为:-0.4619804800000001
第7次迭代,损失为:10.291749533446596
w的值为:-0.21058438400000007
第8次迭代,损失为:6.651429701405821
w的值为:-0.00946750720000003
第9次迭代,损失为:4.3216250088997255
w的值为:0.15142599423999997
第10次迭代,损失为:2.830550005695824
w的值为:0.280140795392
第11次迭代,损失为:1.8762620036453272
w的值为:0.3831126363136
第12次迭代,损失为:1.2655176823330097
w的值为:0.46549010905088
第13次迭代,损失为:0.8746413166931264
...
第999次迭代,损失为:0.1797499999999994
w的值为:0.7949999999999997
第1000次迭代,损失为:0.1797499999999994
w的值为:0.7949999999999997
|
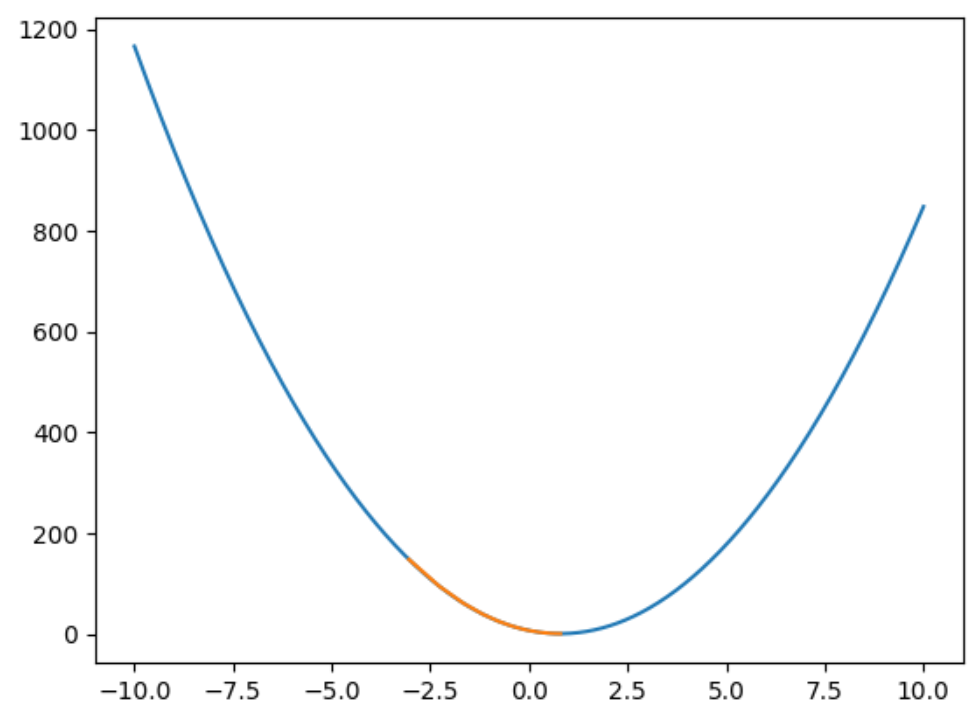
这里只有一个回归系数w,接下来我们看看两个以上w的情况:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| import numpy as np
x=np.array([[3,3],
[5, 1],
[7, 4],
[8, 0],
[0, 1],
[8, 8],
[7, 2],
[9, 9],
[8, 6],
[2, 8]])
y=np.array([15, 13, 16, 14, 12, 10, 16, 26, 18, 17])
w1=1
w2=5
def loss(w1,w2):
e=((3*w1+3*w2)-15)**2+((5*w1+1*w2)-13)**2+((7*w1+4*w2)-16)**2+((8*w1+0*w2)-14)**2+((0*w1+1*w2)-12)**2+((8*w1+8*w2)-10)**2+((7*w1+2*w2)-16)**2+((9*w1+9*w2)-26)**2+((8*w1+6*w2)-18)**2
return e/10
def grad_w2(w1,w2):
return 2*176*w2-954+402*w1
def grad_w1(w1,w2):
return 2*341*w1+402*w2-1512
for i in range(100):
w1,w2=w1-0.01*grad_w1(w1,w2),w2-0.01*grad_w2(w1,w2)
print("w1:",w1,"w2:",w2,"loss:",loss(w1,w2))
|
结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| w1: -10.8 w2: -7.08 loss: 12614.35488
w1: 106.4376 w2: 70.7976 loss: 913017.8629334399
w1: -888.9531840000002 w2: -596.7491040000001 loss: 66203290.0992522
w1: 7587.758928960002 w2: 5086.939541760001 loss: 4800575884.017927
w1: -64595.13392442242 w2: -43312.33853965441 loss: 348103377262.68176
w1: 550074.4003695493 w2: 368829.07149610727 loss: 25241956304557.883
w1: -4684110.757565128 w2: -3140738.809655779 loss: 1830365408894084.0
w1: 39887309.743845284 w2: 26744796.585744374 loss: 1.3272495506359352e+17
w1: -339658209.86387193 w2: -227743863.02633387 loss: 9.624260609158361e+18
w1: 2892341125.893596 w2: 1939340548.0191264 loss: 6.978822650445428e+20
w1: -24629574340.61762 w2: -16514349497.560455 loss: 5.0605410186368e+22
w1: 209731807657.70758 w2: 140627049592.67517 loss: 3.669540936056161e+24
w1: -1785959859915.2925 w2: -1197502031747.9858 loss: 2.660887567515556e+26
w1: 15208244552349.025 w2: 10197263756873.94 loss: 1.9294845786809373e+28
w1: -129504983597289.44 w2: -86834247767755.86 loss: 1.3991236551357197e+30
w1: 1102792680562618.0 w2: 739432338435857.9 loss: 1.0145439999829299e+32
w1: -9390771401386570.0 w2: -6296596068720077.0 loss: 7.356744517349455e+33
w1: 7.996660575232454e+16 w2: 5.3618323126748616e+16 loss: 5.33458281695637e+35
w1: -6.809513044480581e+17 w2: -4.565839294037512e+17 loss: 3.8682563685410073e+37
w1: 5.798603988090778e+18 w2: 3.8880157459786465e+18 loss: 2.804981728879671e+39
w1: -4.9377698509522485e+19 w2: -3.310818771199112e+19 loss: 2.033971316724372e+41
w1: 4.204731199276252e+20 w2: 2.8193098104249798e+20 loss: 1.474889934099441e+43
w1: -3.5805161017696206e+21 w2: -2.400768014336148e+21 loss: 1.0694842645131726e+45
w1: 3.0489691129930502e+22 w2: 2.044361012524097e+22 loss: 7.755131861684831e+46
w1: -2.5963331507966425e+23 w2: -1.7408645585792782e+23 loss: 5.62346470983337e+48
...
w1: -2.450714767014284e+90 w2: -1.6432261321213643e+90 loss: 5.0103570084355345e+182
w1: 2.0868928995151016e+91 w2: 1.3992803216343261e+91 loss: 3.633151095703263e+184
w1: -1.7770823568147882e+92 w2: -1.191549586656921e+92 loss: 2.634500268541024e+186
w1: 1.513264865502289e+93 w2: 1.014657603277089e+93 loss: 1.9103504044054218e+188
|
有人说把除了要求导的当前w以外其他回归系数的值全部代入公式,然后求解现在的w。依次类推,求出所有的w。(把多维处理成多个一维)
这样是不可行的,固定一个w,去求解另一个“最优”w,即使算出来了,另一个w也不是最优的,因为所有w之间基本都是相互联系的,不存在固定一个就能求出另一个最优解的情况。再用计算出的“最优”w去求解前一个w,求出来的也不是最优的,这样做的话需要来回求解。
画个图会好理解一些,你把两个w综合成的损失函数想象成一个碗:
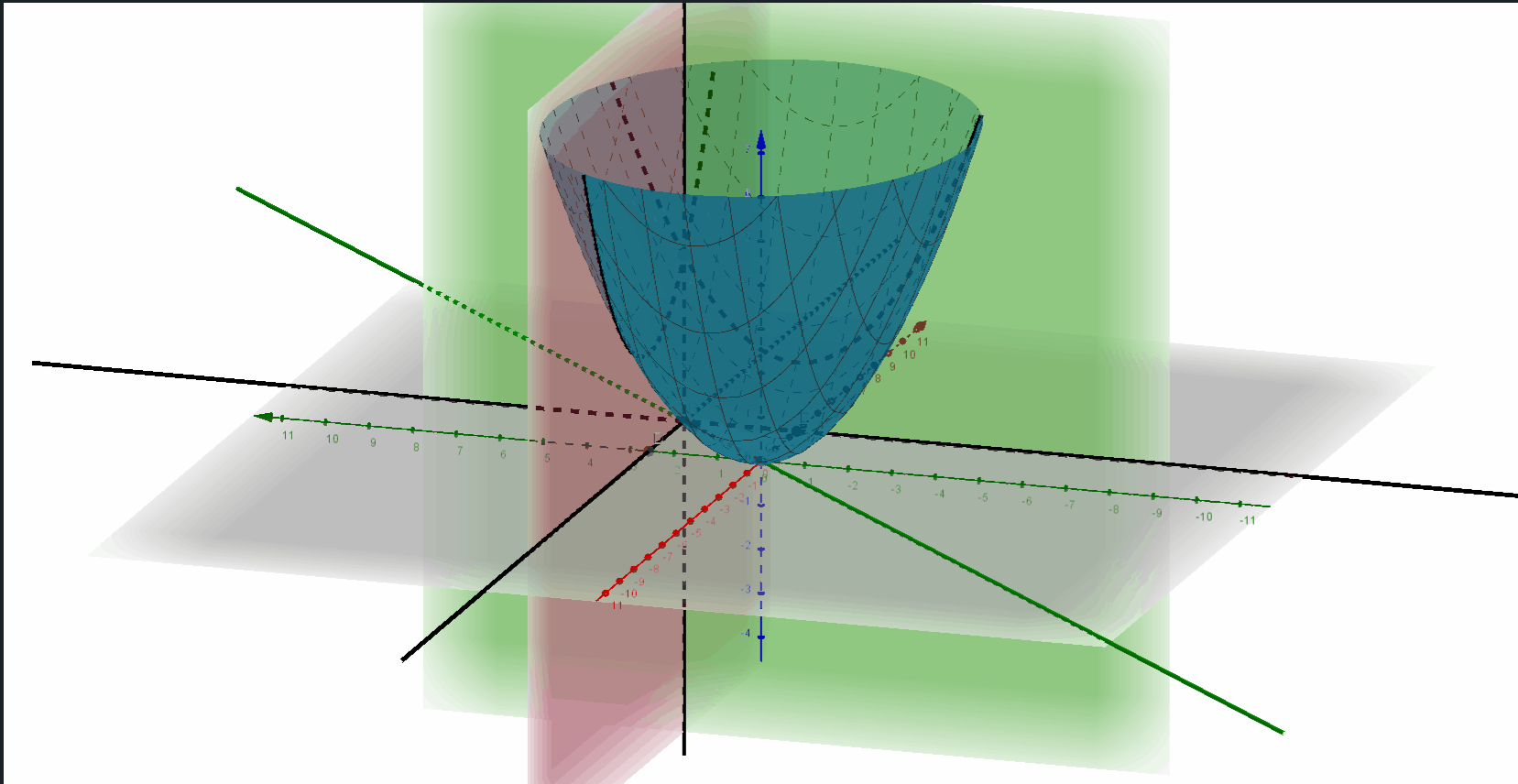
图中就是由两个w的损失函数构建的三维图形,图形上所有点到底部坐标平面的距离就是损失。
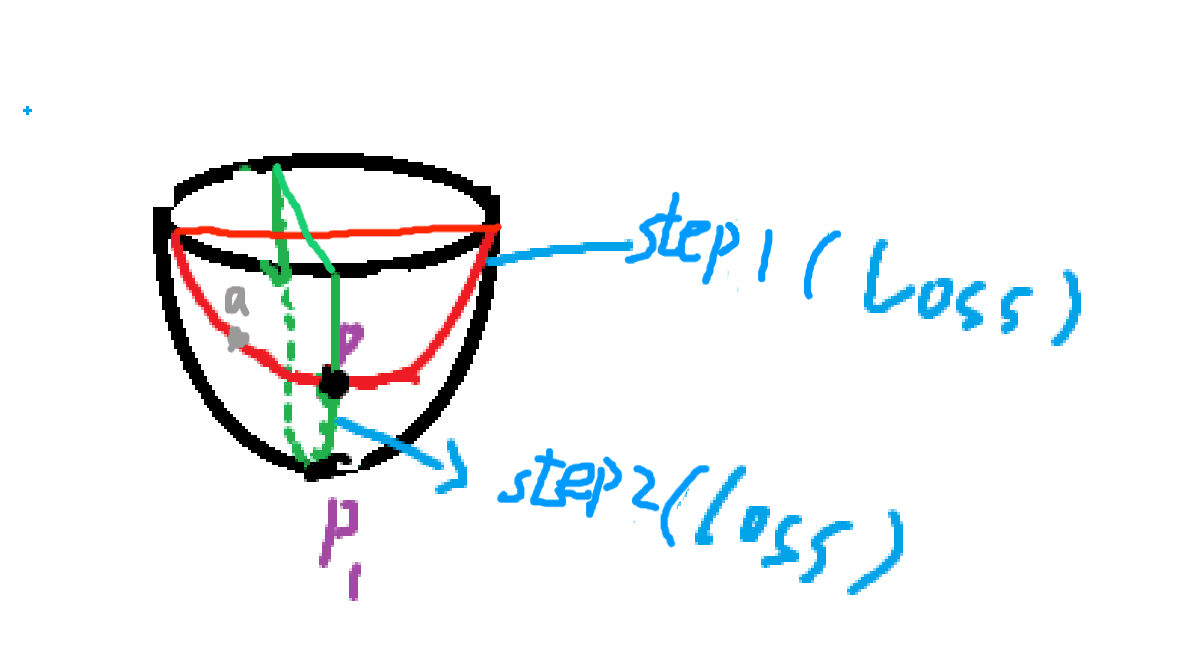
假设条件完全理想,那么图中的操作的确只需要两步就可以做到。但实际情况不会存在,一个w固定,另一个w的优化基本都会被限制。
计算量极大,相当于求不出来。所以一般是多个w一起求解,固定其他所有初始w,求出当前的一个w,依次类推,直到这一轮训练所有w求出。然后下一轮训练,用上一轮训练的所有w去预测,直到损失函数最低,此时的所有w就是最优解。




