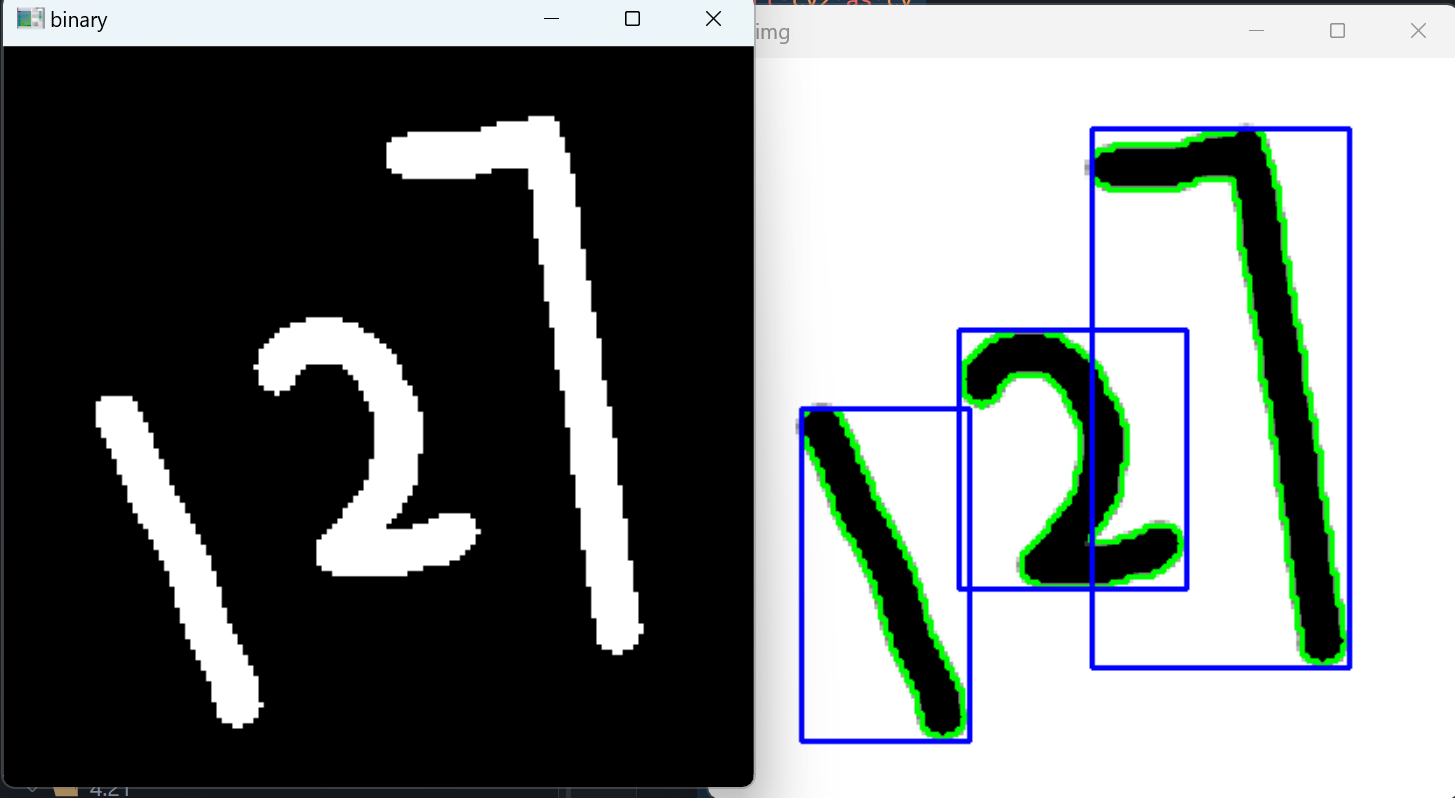
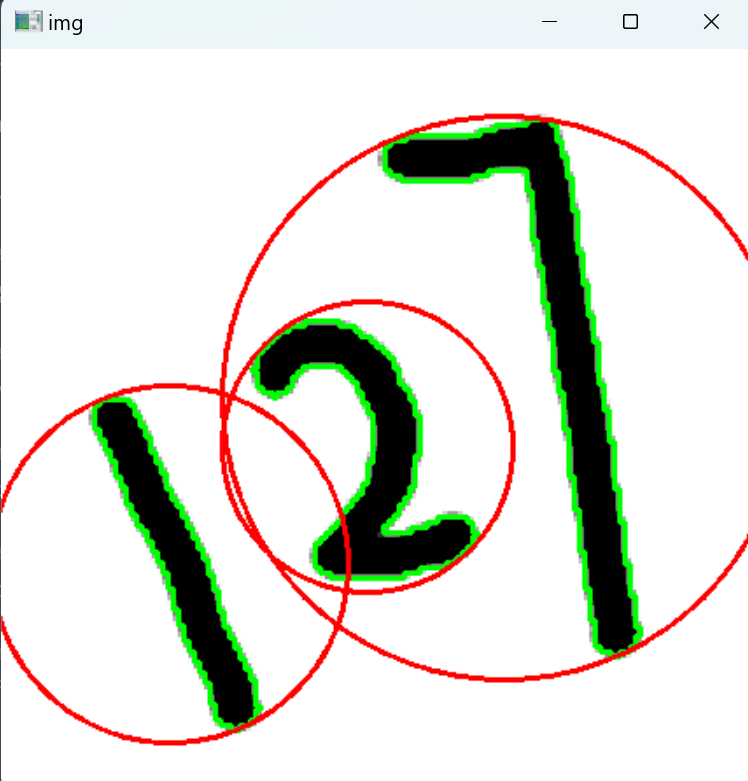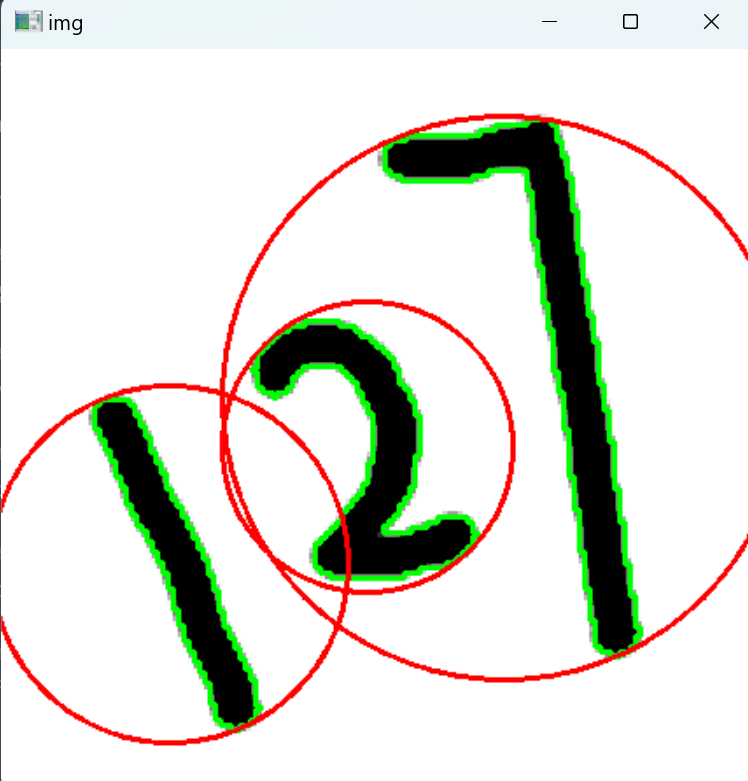其实就是外接轮廓，有了轮廓点就可以找到最上、最下、最左、最右的四个坐标（因为有xmin,xmax,ymin,ymax）。就可以绘制出矩形。

一.外接矩形

cv.boundingRect(轮廓点)

• 返回x,y,w,h，传入一个轮廓的轮廓点，若有多个轮廓需要循环获取。

这是最简单的外接矩形，理论上是方方正正的。

import cv2 as cv
 
num = cv.imread('../images/num.png')
 
# 拷贝
img = num.copy()
 
# 灰度化
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
 
# 二值化
ret, binary = cv.threshold(gray, 0, 255, cv.THRESH_OTSU+cv.THRESH_BINARY_INV)
 
# 轮廓检测
contours, hierarchy = cv.findContours(binary, cv.RETR_EXTERNAL, cv.CHAIN_APPROX_SIMPLE)
 
# 绘制轮廓
cv.drawContours(img, contours, -1, (0, 255, 0), 2)
 
# 获取外接矩形
for cnt in contours:
    x, y, w, h = cv.boundingRect(cnt)
    # 绘制外接矩形
    cv.rectangle(img, (x, y), (x+w, y+h), (255, 0, 0), 2)
 
 
# 绘制图像
cv.imshow('img', img)
cv.imshow('binary', binary)
 
cv.waitKey(0)
cv.destroyAllWindows()

结果：

二.最小外接矩形

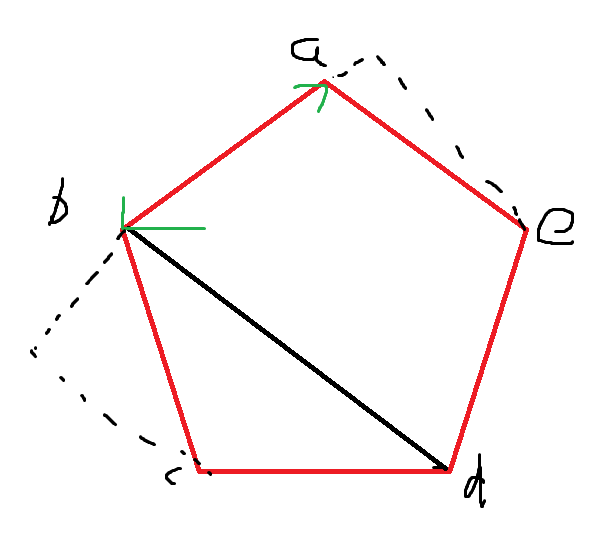
寻找最小外接矩形使用的算法叫做旋转卡壳法,其就是基于凸包点进行的。

而对于凸包多边形的一个最小外接矩形，应存在一条边与原凸包多边形的边共线。

如图，这是一个凸包点的图像，找一条边ab，然后找到离这条边最远的点d，画一条线。然后分别找在向量ab与ba上投影最长的点，找到后平移之前画的直线与投影最长的点重合即可。

rect = cv2.minAreaRect(cnt)

传入的cnt参数为contours中的轮廓也可以是凸包点(不过内部已经自动处理得到凸包了)

• 计算轮廓最小面积外接矩形:

• rect 结构通常返回中心点坐标 (x, y)、宽度 width、高度 height 和旋转角度 angle

cv2.boxPoints(rect).astype(int)

• 返回一个形状为 4行2列的数组，每一行代表一个点的坐标（x, y），顺序按照逆时针或顺时针方向排列

• 而这些坐标一般会是浮点数，需要转换为整数坐标

import cv2 as cv
 
num = cv.imread('../images/num.png')
 
img = num.copy()
 
# 灰度化
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
 
# 二值化
ret, binary = cv.threshold(gray, 0, 255, cv.THRESH_OTSU+cv.THRESH_BINARY_INV)
 
# 轮廓检测
contours, hierarchy = cv.findContours(binary, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
 
# 绘制轮廓
cv.drawContours(img, contours, -1, (0, 255, 0), 2)
 
# 获取最小外接矩形坐标
for cnt in contours:
    # 筛选面积最小的矩形
    rect = cv.minAreaRect(cnt)
    # 计算最小矩形的四个顶点坐标
    box = cv.boxPoints(rect).astype(int)
    # 绘图
    cv.drawContours(img, [box], 0, (0, 0, 255), 2)
 
cv.imshow('img', img)
cv.waitKey(0)
cv.destroyAllWindows()

结果：

三.最小外接圆

使用的算法是Welzl算法。Welzl算法基于一个定理：希尔伯特圆定理,对于平面上的任意三个不在同一直线上的点，存在一个唯一的圆同时通过这三个点，且该圆是最小面积的圆。

若已经存在平面上互不共线（或共圆）的 n 个点，并确定了它们的最小覆盖圆，那么添加第 n+1 个点，并且要求这个点不在原来的最小覆盖圆内（即在圆外），为了使新的包含 n+1 个点的最小覆盖圆的半径增大，新加入的点必须位于由原 n 个点确定的最小覆盖圆的边界上（即圆周上）。

这是因为，如果新点在原最小覆盖圆的内部，显然不会影响最小覆盖圆；如果新点在原最小覆盖圆之外但不在圆周上，那么通过新点和至少两个原有圆上的点可以构造出一个更大的圆，这个圆必然比原最小覆盖圆更大，因此不是包含所有 n+1 个点的最小覆盖圆。所以，按照这一逻辑，当第 n+1 个点在原 n 个点的最小覆盖圆外时，确实这个点会位于包含所有 n+1 个点的新最小覆盖圆的圆周上。

获取参数的函数：

cv2.minEnclosingCircle(points)

参数说明：

• points：输入参数图片轮廓数据

返回值：

• center：一个包含圆心坐标的二元组 (x, y)。

• radius：浮点数类型，表示计算得到的最小覆盖圆的半径。

import cv2 as cv
 
num = cv.imread('../images/num.png')
 
img = num.copy()
 
# 灰度化
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
 
# 二值化
ret, binary = cv.threshold(gray, 0, 255, cv.THRESH_OTSU+cv.THRESH_BINARY_INV)
 
# 轮廓检测
contours, hierarchy = cv.findContours(binary, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
 
# 绘制轮廓
cv.drawContours(img, contours, -1, (0, 255, 0), 2)
 
# 获取最小外接圆
for cnt in contours:
    (x, y), radius = cv.minEnclosingCircle(cnt)
    center = (int(x), int(y))
    radius = int(radius)
    cv.circle(img, center, radius, (0, 0, 255), 2)
 
cv.imshow('img', img)
cv.waitKey(0)
cv.destroyAllWindows()

结果：