机器学习-线性回归
最后更新时间:
文章总字数:
预计阅读时间:
线性回归
一.前瞻概念
分类的目标变量是标称型数据,回归是对连续型的数据做出预测
标称数据的特点:
无序性:标称数据的各个类别之间没有固有的顺序关系。例如,“性别”可以分为“男”和“女”,但“男”和“女”之间不存在大小、高低等顺序关系。
非数值性:标称数据不能进行数学运算,因为它们没有数值含义。你不能对“颜色”或“品牌”这样的标称数据进行加减乘除。
多样性:标称数据可以有很多不同的类别,具体取决于研究的主题或数据收集的目的。
比如西瓜的颜色,纹理,敲击声响这些数据就属于标称型数据,适用于西瓜分类
连续型数据(Continuous Data)表示在某个范围内可以取任意数值的测量,这些数据点之间有明确的数值关系和距离。例如,温度、高度、重量等
连续型数据的特点包括:
可测量性:连续型数据通常来源于物理测量,如长度、重量、温度、时间等,这些量是可以精确测量的。
无限可分性:连续型数据的取值范围理论上是无限可分的,可以无限精确地细分。例如,你可以测量一个物体的长度为2.5米,也可以更精确地测量为2.53米,甚至2.5376米,等等。
数值运算:连续型数据可以进行数学运算,如加、减、乘、除以及求平均值、中位数、标准差等统计量。
比如西瓜的甜度,大小,价格这些数据就属于连续型数据,可以用于做回归
二.回归
回归的目的是预测数值型的目标值y,就相当于求一个y = f(x)函数,比如y = ax + b,求解a、b(回归系数)的过程就是回归。
三.线性回归
线性回归是机器学习中一种有监督学习的算法,一般求解的都是多元一次方程。
我们来介绍一下基本参数:
需要预测的值(标签):target,y
影响目标变量的因素(特征):X1,X2…Xn,可以是连续值也可以是离散值
因变量和自变量之间的关系(模型):model,就是我们要求解的线性回归方程
先看一个最简单的,y = ax + b,很经典的线性回归方程,只要确定了a和b就可以完成预测。然而现实数据集中很难得到完美拟合数据的参数,所以我们会选取参数能让预测值最接近真实值。
四.损失函数
什么是损失函数呢?如图:
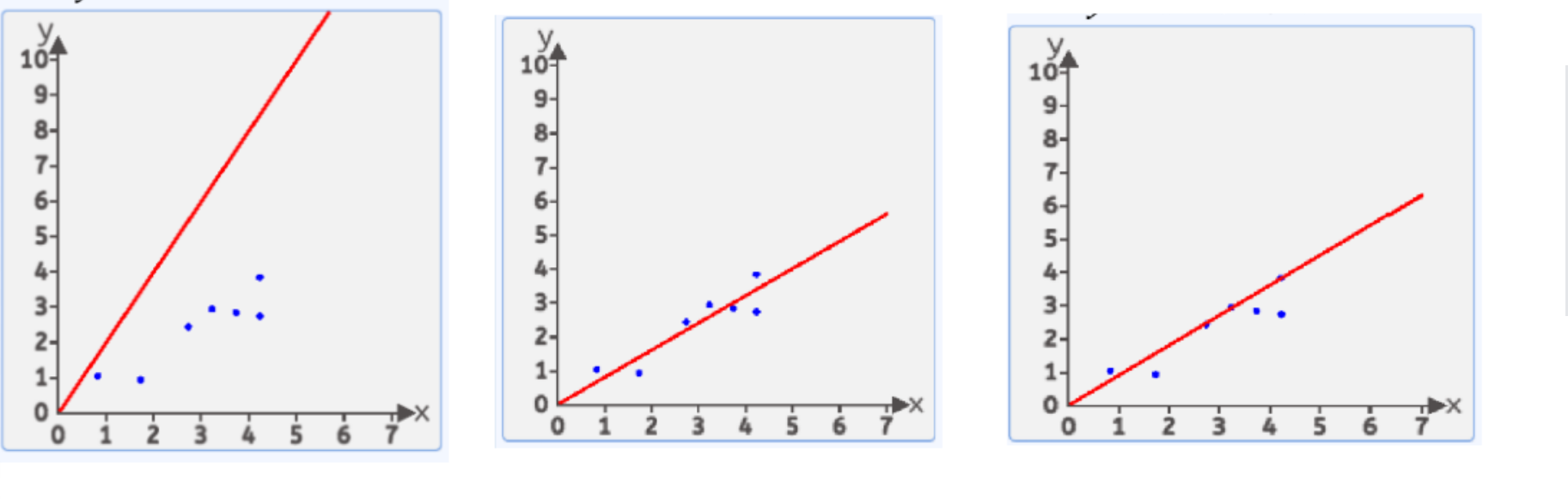
红色的便是回归直线,蓝色就是真实数据点,而我们的目的是让回归直线预测值更接近真实值,也就是尽可能让每个数据的预测值与真实值的差距最小。注意,这里的差距是图中数据点与回归直线的竖直距离,因为这样表示的才是预测值y^与真实值y的差距。
那怎样做呢?这就是损失函数的事儿了:
我们有很多方式认为某条直线是最优的,其中有一种方式叫均方差(MSE),其将所有数据的预测值与真实值之差的平方相加再求均值:
$$
MSE = \frac{1}{n}\sum_{i=1}^n(y_i-\hat{y}_i)^2
$$
还有一种叫MAE,就是取所有数据的预测值与真实值之差的绝对值相加再求均值:
$$
MAE = \frac{1}{n}\sum_{i=1}^n|y_i-\hat{y}_i|
$$
我们以MSE为例:
假设回归直线为 y = wx(此处先不加b参数)。那么根据均方差损失函数的公式,把已知的真实数据代入其中就可以得到:
loss = aw^2+bw+c
其中,a,b,c为常数,w为回归系数,这就是损失函数。
此处的自变量是w即回归直线的斜率,因为假设b = 0,所以整个损失函数方程就是一个抛物线,我们只需要找到抛物线最低点的w就可以了。而均方差这种取损失函数的方式让输入所有数据后的整个方程变为一元二次或多元二次方程。说白了,有再多的参数(特征),也就是通过输入的数据来计算损失函数loss中的所有参数,使得损失函数最小。
于是就明白了,损失函数就是衡量线性回归方程(模型)好坏的指标,也是计算回归方程(也可以说所有机器学习中方程)的方法。
五.多参数回归
实际情况下,我们的数据一般不会只用一个特征来预测目标。实际情况下,往往影响结果y的因素不止1个,这时x就从一个变成了n个,x1,x2,x3…xn。
相对的,损失函数就会有w1,w2,w3…wn,并且可能还会有不变的特征(常数)b。也就和之前讲过的一样,通过输入的数据来计算损失函数loss中的所有参数,使得损失函数最小。
那么损失函数就是
$loss=[(y_1-y_1^,)^2+(y_2-y_2^,)^2+….(y_n-y_n^,)^2]/n$